Çoxluq nəzəriyyəsi – riyaziyyatın çoxluqların ümumi xassələrini öyrənən bölməsi. Bir çox riyazi fənnlər, o cümlədən cəbr, analiz, ölçü nəzəriyyəsi, stoxastik və topologiya çoxluq nəzəriyyəsinə əsaslanırlar.Əsası alman riyaziyyatçısı Qeorq Kantor tərəfindən qoyulmuşdur.
Mündəricat
[gizlə]Anlayışlar![redaktə | əsas redaktə]
Hər hansı bir çoxluğu təşkil edən obyektlərə bu çoxluğun elemnti deyilir. Çoxluqlar böyük hərflərlə işarə olunur. elemntlər isə uyğun kiçik hərflərlə işarə olunur.
Çoxluq nəzəriyyəsində 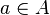 münasibəti o deməkdir ki,
münasibəti o deməkdir ki, 
 çoxluğunun elementidir. Bunun inkarı isə
çoxluğunun elementidir. Bunun inkarı isə  kimi işarə edililirlər. Bu münasibət isə onu göstərir ki,
kimi işarə edililirlər. Bu münasibət isə onu göstərir ki, 
 çoxluğunun elementi deyil.
çoxluğunun elementi deyil.
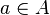 münasibəti o deməkdir ki,
münasibəti o deməkdir ki, 
 çoxluğunun elementidir. Bunun inkarı isə
çoxluğunun elementidir. Bunun inkarı isə  kimi işarə edililirlər. Bu münasibət isə onu göstərir ki,
kimi işarə edililirlər. Bu münasibət isə onu göstərir ki, 
 çoxluğunun elementi deyil.
çoxluğunun elementi deyil.Dəqiq Alt Çoxluğu[redaktə | əsas redaktə]
Bir çoxluq  digər çoxluğun
digər çoxluğun  o vaxt dəqiq altçoxluğu adlanır ki,
o vaxt dəqiq altçoxluğu adlanır ki,  çoxluğuna aid olan ixtiyari element həm də
çoxluğuna aid olan ixtiyari element həm də  çoxluğunun elementi olsun.
çoxluğunun elementi olsun.
 digər çoxluğun
digər çoxluğun  o vaxt dəqiq altçoxluğu adlanır ki,
o vaxt dəqiq altçoxluğu adlanır ki,  çoxluğuna aid olan ixtiyari element həm də
çoxluğuna aid olan ixtiyari element həm də  çoxluğunun elementi olsun.
çoxluğunun elementi olsun. o zaman
o zaman  -nin üstçoxluğu adlanır. Formal olaraq:
-nin üstçoxluğu adlanır. Formal olaraq: .
.
Bərabərlik[redaktə | əsas redaktə]
İki çoxluq o zaman bərabərdirlər ki, onlar eyni elementlərə malik olsunlar.
Bu analyış çoxluq nəzəriyyəsinin əsası hesab olunur. Formal olaraq belə ifadə olunur:
Boş çoxluq[redaktə | əsas redaktə]
Tərkibində heç bir element olmayan çoxluq boş çoxluq adlanır. O  və ya
və ya  ilə işarə olunur. Bərabərlik qanunundan alınır ki, yalnız bir nir boş çoxluq mövcuddur. Digər boş çoxluqlar elə həmin elementləri əhatə edirlər, yəni bərabərdirlər. Uyğun olaraq:
ilə işarə olunur. Bərabərlik qanunundan alınır ki, yalnız bir nir boş çoxluq mövcuddur. Digər boş çoxluqlar elə həmin elementləri əhatə edirlər, yəni bərabərdirlər. Uyğun olaraq:  və
və  müxtəlif olurlar. Çünki sonuncu çoxluq birincidən fərqli olan elementə sahibdir. Boş çoxluq hər bir çoxluğun alt çoxluğudur. Boş çoxluğu həmçinin aşağıdakı kimi də ifadə etmək olar:
müxtəlif olurlar. Çünki sonuncu çoxluq birincidən fərqli olan elementə sahibdir. Boş çoxluq hər bir çoxluğun alt çoxluğudur. Boş çoxluğu həmçinin aşağıdakı kimi də ifadə etmək olar:
 və ya
və ya  ilə işarə olunur. Bərabərlik qanunundan alınır ki, yalnız bir nir boş çoxluq mövcuddur. Digər boş çoxluqlar elə həmin elementləri əhatə edirlər, yəni bərabərdirlər. Uyğun olaraq:
ilə işarə olunur. Bərabərlik qanunundan alınır ki, yalnız bir nir boş çoxluq mövcuddur. Digər boş çoxluqlar elə həmin elementləri əhatə edirlər, yəni bərabərdirlər. Uyğun olaraq:  və
və  müxtəlif olurlar. Çünki sonuncu çoxluq birincidən fərqli olan elementə sahibdir. Boş çoxluq hər bir çoxluğun alt çoxluğudur. Boş çoxluğu həmçinin aşağıdakı kimi də ifadə etmək olar:
müxtəlif olurlar. Çünki sonuncu çoxluq birincidən fərqli olan elementə sahibdir. Boş çoxluq hər bir çoxluğun alt çoxluğudur. Boş çoxluğu həmçinin aşağıdakı kimi də ifadə etmək olar: - A çoxluğunun boş alt çoxluğudur. Aşkar
- A çoxluğunun boş alt çoxluğudur. Aşkar
Çoxluqların kəsişməsi[redaktə | əsas redaktə]
Bir qeyri-xətti  çoxluğu verilir. Bu çoxluqdan yaranmış kəsişmə çoxluğu A və B çoxluqlarına aid olan elemntlərdən təşkil olunur. Daha dəqiq desək, A və B çoxluqlarının kəsişməsindən yaranan çoxluğun elementləri, bu hər iki çoxluğun altçoxluğudur. Formal olaraq:
çoxluğu verilir. Bu çoxluqdan yaranmış kəsişmə çoxluğu A və B çoxluqlarına aid olan elemntlərdən təşkil olunur. Daha dəqiq desək, A və B çoxluqlarının kəsişməsindən yaranan çoxluğun elementləri, bu hər iki çoxluğun altçoxluğudur. Formal olaraq:
 çoxluğu verilir. Bu çoxluqdan yaranmış kəsişmə çoxluğu A və B çoxluqlarına aid olan elemntlərdən təşkil olunur. Daha dəqiq desək, A və B çoxluqlarının kəsişməsindən yaranan çoxluğun elementləri, bu hər iki çoxluğun altçoxluğudur. Formal olaraq:
çoxluğu verilir. Bu çoxluqdan yaranmış kəsişmə çoxluğu A və B çoxluqlarına aid olan elemntlərdən təşkil olunur. Daha dəqiq desək, A və B çoxluqlarının kəsişməsindən yaranan çoxluğun elementləri, bu hər iki çoxluğun altçoxluğudur. Formal olaraq: .
.
Çoxluqların birləşməsi[redaktə | əsas redaktə]
 .
.





Комментариев нет:
Отправить комментарий